This is already the Part-3 lessons for Series-Parallel Circuits. Today we will be dealing with another type of complex circuit which you do not know yet - particularly for the beginners.
Suppose you have a type of simple circuit below. You will notice that there is an extra resistor of R3 connecting to the two parallel branches of the parallel circuit connection and in such way it was interrupted to the leads of the new resistor. This new resistor (R3) is called a bridge.
Take a look at the circuit above. If you look at the upper part of R3 resistor, wherein R1, R2 and R3 are all connected together. You will notice a new arrangement of connection. This arrangement from its similarity to the shape of the Greek letter D (delta), is said to be delta connected. Here is the diagram below to see clearly what I'm talking about.
Take a look at the diagram at the left side. If you will devise a circuit shown in the delta connection Ra, Rb and Rc to shaped like a Y (wye). This Y circuit would fit onto the rest of the original circuit in such a way that you could solve its values without difficulty. Look at the diagram (at the left) in Y connection.
The resistors connected in Y are R1, R2 and R3. Take note that their values must be such that the terminal resistances at N1 and N3 are exactly where they were in the original circuit. The problem now is how would you able to solve the values of R1, R2 and R3 (said to be unknown values) in terms of Ra, Rb and Rc whose values are known.
How to Solve Bridge Resistor Circuit
Lets use again this previous diagram. Then, take note that both circuits must give exactly the same values of resistance across every corresponding pair of terminals. This operation that we'll set is called delta-Y conversion or transformation.
If you consider the sum of the resistances between N3 and N1, then assume N2 is to be disconnected. In delta combination you will see that between these two points there is a series combination of Rc and Rb in parallel across Ra. You can now express the resistance N3 and N1 applying the knowledge of parallel circuits we have:
Suppose you have a type of simple circuit below. You will notice that there is an extra resistor of R3 connecting to the two parallel branches of the parallel circuit connection and in such way it was interrupted to the leads of the new resistor. This new resistor (R3) is called a bridge.
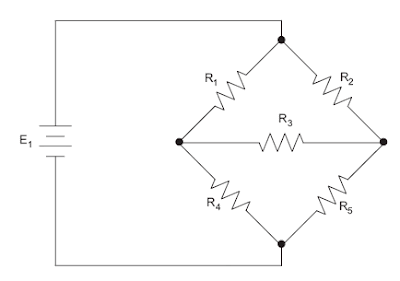 |
| R3 is called the Bridge Resistor |
 |
| This is the illustrative diagram for delta connection |
 |
| The equivalent connection of left diagram is called the Y connection |
The resistors connected in Y are R1, R2 and R3. Take note that their values must be such that the terminal resistances at N1 and N3 are exactly where they were in the original circuit. The problem now is how would you able to solve the values of R1, R2 and R3 (said to be unknown values) in terms of Ra, Rb and Rc whose values are known.
How to Solve Bridge Resistor Circuit
Lets use again this previous diagram. Then, take note that both circuits must give exactly the same values of resistance across every corresponding pair of terminals. This operation that we'll set is called delta-Y conversion or transformation.
 |
| delta -Y conversion |
Ra (Rb + Rc) / Ra + Rb + Rc
Considering the Y circuit connection above, the total resistance between N3 and N1 is R1 + R3. Then, since we all know that these resistances must be equal, you can now write down the first equation as:
R1 + R3 = Ra (Rb + Rc)/ Ra + Rb + Rc ---------> EQUATION no. 1
For the remaining terminals, you can exactly do the same way for total resistances between N3 - N2 and between N1 - N2 in terms of Ra, Rb, Rc and R1, R2 and R3. Then, you will get the two remaining equations:
R2 + R3 = Rc (Ra + Rb) / Ra + Rb + Rc ---------> EQUATION no. 2
R1 + R2 = Rb (Ra + Rc) / Ra + Rb + Rc ---------> EQUATION no. 3
Then, do a little algebra from the three equations above to obtain the values in terms of R1, R2 and R3. Finally, we can have the following formula:
R1 = Ra x Rb / Ra + Rb + Rc ------------> Formula no. 1
R2 = Rb x Rc / Ra + Rb + Rc ------------> Formula no. 2
R3 = Ra x Rc / Ra + Rb + Rc ------------> Formula no. 3
The problem below was given in the board exam way back 1997 - two years before my EE board examination.
(EE April'97) A circuit consisting of three resistors rated : 10 ohms, 15 ohms and 20 ohms are connected in DELTA. What would be the resistances of the equivalent WYE connected load?
Solution:
Just get the pattern of the above formula, this would give us the following:
R1 = 10 X 15 / 10 + 15 + 20 = 3. 33 ohms - answer
R2 = 15 x 20 / 10 + 15 + 20 = 6. 67 ohms - answer
R3 = 10 X 20 / 10 + 15 + 20 = 4.44 ohms - answer
Y to Delta Conversion
For the reverse conversion which is Y to delta conversion considering the given circuit.
 |
| Y to delta conversion or transformation |
The general idea here is to compute the resistance in the delta circuit by:
R- delta = Rp / R opposite
where: Rp is the sum of the product of all pairs of resistances in the Y circuit and R opposite is the resistance of the node in the Y circuit which is opposite the edge with R- delta. You will have the following formula for you to get the equivalent delta load in terms of Ra, Rb and Rc.
Ra = R1R2 + R2R3 + R3R1 / R2 ---------> Formula no. 4
Rb = R1R2 + R2R3 + R3R1 / R3 ---------> Formula no. 5
Rc = R1R2 + R2R3 + R3R1 / R1 ---------> Formula no. 6
These are the formula that you'll going to use from our future topics since this is already the part of Network Theorems. Don't ever forget it...
Cheers!






2 comments:
I was searching for article on bridge resistor circuit and I found your post. It will be very useful for me for my assignment.
Consider this reduction
Valid current paths _through_ the bridge resistor R3
R1+R3+R5
R2+R3+R4 which flows in the opposite direction through R3
Compute the simple series voltage /resistance currents going through R3 and subtract them. That gives you the net current flow through R3. Which should be enough to solve for voltage at B and C.
Post a Comment